Parallel Lines Have The Same
Parallel lines have the same slope and will never intersect. Parallel lines proceed, literally, forever without touching (assuming that these lines are on the same aeroplane).
Parallel Lines in greater depth
On the other hand, the slope of perpendicular lines are the negative reciprocals of each other, and a pair of these lines intersects at 90 degrees.
Perpendicular Lines in greater depth
Parallel Case
As you can see from the diagram below, these lines:
- have the same slope
- two
- are never going to intersect

Perpendicular Instance
Every bit you can meet from the pic below:
- the gradient of these lines are negative reciprocals
- $$\frac{2}{3}$$ and $$-\frac{3}{ii}$$ are negative reciprocals
- these lines are perpendicular and intersect at 90 degrees

Parallel Lines in Greater Depth
Both of the lines below have the same slope: $$ \frac{i}{ii} $$
Therefore these lines are parallel and will never meet.

Problem 1
Are the two lines pictured below parallel?

No.
While these lines may look parallel at first glance, if you expect closely and calculate each line's gradient, you will find that:
- line 1 has a gradient of $$ -\frac{i}{4} $$
- line 2 's slope is $$ - \frac{i}{three} $$
Problem 2
Are the two lines beneath parallel?

Yes these lines have the same slope, 2, and clearly are never going to intersect.
Perpendicular Lines in Greater Depth
Perpendicular lines:
- intersect at $$ xc^{\circ} $$
- have slopes that are negative reciprocals

Trouble 3
Are the two lines in the moving picture below perpendicular?

Yeah
The slope of line one is -2 and that of line 2 is $$ \frac{ane}{two}$$.
-ii and $$ \frac{1}{two}$$ are negative reciprocals and so the lines are perpendicular.
Problem 4
Determine whether or non lines 6 and five perpendicular?
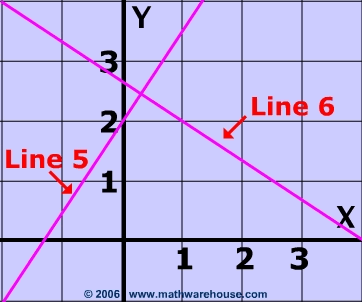
Problem 5
Are line P and line 50 perpendicular?

Parallel Lines Have The Same,
Source: https://www.mathwarehouse.com/algebra/linear_equation/parallel-perpendicular-lines.php
Posted by: danielssoing1993.blogspot.com


0 Response to "Parallel Lines Have The Same"
Post a Comment